Radians In Terms Of Pi - Your Angle Guide

When we talk about measuring angles, you might usually think of degrees, like a full circle having 360 degrees, or perhaps a right angle being 90 degrees. However, there is another way to express how much an angle turns, and it is a system often used in more advanced mathematics and science. This other way involves something called radians, and they have a very special connection to a well-known number called pi. It's almost like having two different languages to describe the same idea, and each one has its own strengths, you know.

This different way of looking at angles, using radians, helps us out in many situations, especially when we are working with circles or things that move in a circular path. It can seem a little bit unusual at first, particularly since it brings pi into the picture in a very direct manner. Yet, once you get a feel for it, this method can actually make certain calculations much simpler to work with, in a way.

So, if you have ever wondered how these two ways of measuring angles relate, or if you have been trying to figure out how many radians are in a full circle, or even how to express degrees to radians in terms of pi, then you have, in all likelihood, come to the right place for some answers. We will explore how these angle measurements connect, especially focusing on how radians come to be expressed with pi, and what that truly means for understanding angles, too.

• All About Fritz The Rising Star In The Entertainment Industry
• Did One Of The American Pickers Die Uncovering The Truth Behind The Rumors
• Did Frank Fritz From American Pickers Die A Comprehensive Overview
• Exploring The Life And Achievements Of Luke Rubenfeld
• Carlos Alman The Journey Of A Rising Star

Table of Contents

• What Exactly Are Radians and Degrees?
  • Understanding Radians in Terms of Pi
• Why Do We Have Two Ways to Measure Angles?
  • Making Sense of Radians in Terms of Pi
• How Does Pi Fit into Radians?
  • Connecting Degrees to Radians in Terms of Pi
• Converting Angles- Degrees to Radians in Terms of Pi
  • Using a Converter for Radians in Terms of Pi

What Exactly Are Radians and Degrees?

When we talk about angles, we are essentially describing a measure of rotation or the amount of turn between two lines that meet at a point. For many people, the most familiar way to talk about this is with degrees. We usually learn that a full circle, a complete spin around, contains 360 of these degrees. This system has been around for a very long time, and it is pretty intuitive for everyday use, you know. It makes sense to divide a circle into 360 equal parts, especially for things like compass directions or telling time.

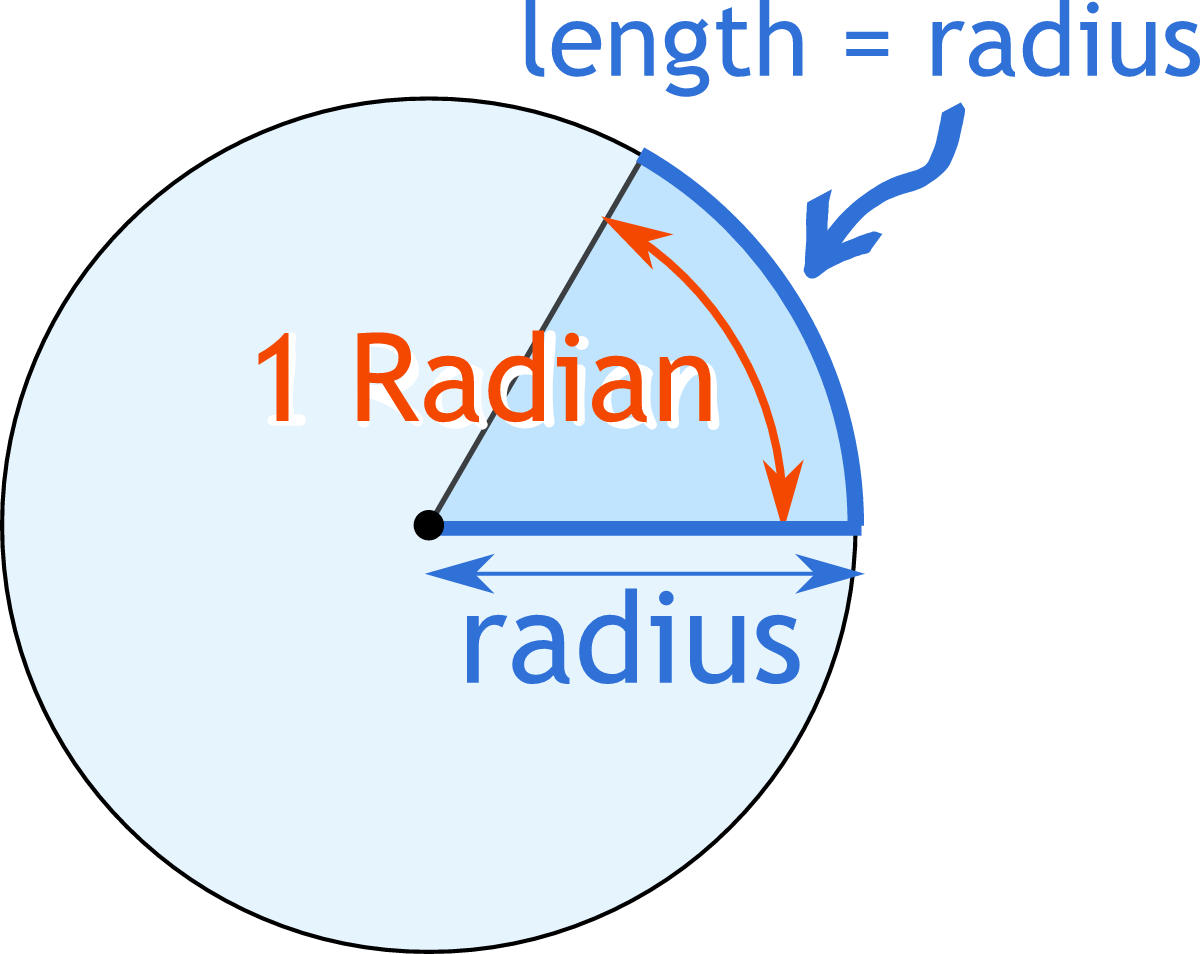
On the other hand, radians offer a different way to think about these turns, one that is more naturally tied to the geometry of a circle itself. Imagine a circle, any circle at all. Now, picture its radius, which is the distance from the very center of the circle out to its edge. A radian is the angle you get when you take that radius and wrap it around the edge of the circle. So, if you were to measure an arc along the circle's edge that has the same length as the radius, the angle formed by that arc back to the center is one radian. It is a measurement that feels, in a way, more organic to the circle's shape, actually.

This means that degrees and radians are simply two distinct systems for expressing the same thing: the size of an angle. While degrees are often used in things like construction or surveying, radians tend to show up more in areas like physics, engineering, and higher-level math. Each system has its own place where it shines brightest, so.

• Movierulz Adult Movie Everything You Need To Know
• Frank Fritz Is He Still Alive
• Tia Kemp Birthday Celebrating The Life And Achievements Of A Remarkable Individual
• The Story Of Aubreigh Wyatt A Journey Of Courage And Resilience
• Jey Uso Lives Where A Deep Dive Into The Life Of The Wwe Superstar

Understanding Radians in Terms of Pi

Now, here is where pi enters the picture when we are discussing radians in terms of pi. Pi, that famous number, is roughly 3.14159, and it describes the relationship between a circle's circumference (the distance around it) and its diameter (the distance across it, through the center). Specifically, the circumference of any circle is always pi times its diameter, or two times pi times its radius. This connection is quite fundamental to how radians work, you know.

Because a radian is defined by the radius wrapping around the circumference, there is a natural link between the total number of radians in a circle and pi. If you think about it, the entire circumference of a circle is 2π times its radius. Since one radian is the angle that corresponds to an arc length equal to one radius, it stands to reason that a full circle must contain 2π radians. This means that going all the way around a circle, which is 360 degrees, is the same as turning 2π radians. This relationship is pretty important, as a matter of fact.

So, when we talk about radians in terms of pi, we are really just saying that we are expressing these angle measurements as a fraction or multiple of this 2π value that represents a whole circle. For example, half a circle, which is 180 degrees, would be π radians. A quarter of a circle, 90 degrees, would be π/2 radians. This way of expressing angles ties them directly to the properties of circles themselves, making calculations involving circular motion or waves much more straightforward, in some respects.

Why Do We Have Two Ways to Measure Angles?

It might seem a little odd that we have two different systems for measuring angles, doesn't it? Why not just stick to one, like degrees, which everyone seems to know? The truth is, both degrees and radians serve different purposes and are useful in different situations. Degrees are very intuitive for everyday geometry and for things like setting angles on a protractor or describing directions. They are, you know, what most people learn first and what feels natural for drawing shapes or talking about turns in a simple way.

Radians, however, are what we call a "natural" unit for measuring angles, especially when we are doing calculations that involve the geometry of circles. When you are dealing with things like the speed of a spinning object, or how waves move, or even the way light bends, using radians often simplifies the formulas involved. Many important equations in physics and engineering become much neater and easier to handle when angles are expressed in radians instead of degrees. It is, quite literally, a mathematical convenience that makes complex problems more manageable, so.

Consider, for instance, how the length of an arc on a circle can be found by simply multiplying the radius by the angle in radians. If you were using degrees, you would need to include an extra conversion factor in your formula, which just adds more steps and potential for mistakes. So, while degrees are great for visual understanding, radians are often better for the actual mathematical work, you know, when precision and simplicity in equations are key.

Making Sense of Radians in Terms of Pi

The fact that radians are expressed in terms of pi can sometimes make them feel a little less straightforward for practical applications, especially if you are used to working with whole numbers for degrees. For example, saying an angle is "π/4 radians" might not immediately give you a clear visual of the turn, compared to saying "45 degrees." That is pretty normal, by the way. Our brains are just more accustomed to the degree system from early on.

However, this connection to pi is precisely what makes radians so powerful in higher-level math. Pi is fundamental to circles, and because radians are defined by the radius and the arc length, they naturally incorporate pi into their very definition. This means that when you are working with formulas that describe circular motion, oscillations, or even the properties of waves, the pi is already built into the angle unit. This eliminates the need for constant conversion factors in your equations, which can make things much cleaner and more elegant, you know.

So, while the presence of pi might make radians seem a bit abstract at first, it is actually a sign of their deep connection to the underlying geometry of the universe. It is a bit like how some measurements are just inherently linked to certain constants. This is why, for many scientific and engineering problems, expressing angles as radians in terms of pi is the preferred method, even if it takes a little getting used to, in some respects.

How Does Pi Fit into Radians?

The relationship between pi and radians is at the very core of what a radian is. As we discussed, a full circle measures 360 degrees. In the radian system, this same full circle is equivalent to 2π radians. This is not just a random conversion factor; it comes directly from the definition of a radian and the properties of circles. The circumference of a circle is 2π times its radius. Since one radian is the angle subtended by an arc equal to the radius, you can fit exactly 2π such "radius lengths" around the entire circumference. This makes the connection very direct, you know.

So, when you see an angle expressed as a multiple or fraction of pi, you are looking at it in radians. For example, if you have an angle of π radians, that is half a circle, because a full circle is 2π radians. Similarly, if you have an angle of π/2 radians, that is a quarter of a circle. This system means that angles are always expressed in relation to the fundamental constant of circles, which is pi. It is a very consistent way of measuring turns, actually.

This direct link to pi is what gives radians their unique character and makes them so valuable in many fields. It is a way of measuring angles that is inherently tied to the geometry of circles, rather than an arbitrary division of a circle into 360 parts. This is why you will often see angles written with π right in them when you are dealing with things like trigonometry or calculus, so.

Connecting Degrees to Radians in Terms of Pi

Since we have two different ways to measure angles, there needs to be a way to switch between them. This is where the conversion formulas come in, and they are pretty straightforward, you know. The key relationship to remember is that 360 degrees is the same as 2π radians. From this, we can easily figure out how to convert any degree measure into radians, especially radians in terms of pi.

If 360 degrees equals 2π radians, then 180 degrees must equal π radians (just divide both sides by two). This gives us a very handy conversion factor. To convert an angle from degrees to radians, you simply multiply the angle in degrees by the fraction π/180. This fraction, π/180, is the bridge between the two systems. It is, in a way, like a language translator for angles, actually.

Let us take an example. If you want to know what 60 degrees is in radians, you would multiply 60 by (π/180). This simplifies to 60π/180, which reduces to π/3 radians. So, 60 degrees is equivalent to π/3 radians. Similarly, 90 degrees would be 90 * (π/180), which simplifies to π/2 radians. This method allows you to express any angle that was originally in degrees as radians in terms of pi, making it ready for use in more advanced calculations, so.

Converting Angles- Degrees to Radians in Terms of Pi

The process of changing an angle from degrees to radians, especially to express it in terms of pi, is a very common task in mathematics. As we have discussed, the core idea is to use the relationship that 180 degrees is the same as π radians. This means our conversion factor is π/180. You just take your degree value and multiply it by this fraction. It is a pretty simple operation, you know, once you get the hang of it.

Let us look at a few more examples to make this idea really stick. Suppose you have an angle of 45 degrees. To convert this to radians in terms of pi, you would multiply 45 by (π/180). This gives you 45π/180. If you simplify this fraction, you will find it reduces to π/4 radians. So, a 45-degree angle is exactly π/4 radians. This is a very common angle to see expressed this way, by the way.

What about a larger angle, like 270 degrees? Using the same method, you would multiply 270 by (π/180). This gives you 270π/180. When you reduce this fraction, you get 3π/2 radians. This makes sense, too, since 270 degrees is three-quarters of a full circle, and a full circle is 2π radians. Three-quarters of 2π is indeed 3π/2. This consistent pattern helps confirm the method, actually.

Even for angles that might not seem like neat fractions of a circle, the method still works. For instance, if you want to find the value of 40 degrees in radians in terms of pi, you multiply 40 by (π/180). This results in 40π/180, which simplifies to 2π/9 radians. So, you can see that any degree measure can be converted into its radian equivalent, expressed using pi, which is pretty useful.

This conversion is a fundamental skill for anyone working with angles in a more advanced setting. It bridges the gap between the familiar degree system and the mathematically elegant radian system, allowing for smoother calculations and a deeper appreciation of how angles relate to the geometry of circles. The fact that it is always expressed in terms of pi means you are always connecting back to the very essence of circular measurement, in a way.

Using a Converter for Radians in Terms of Pi

While knowing how to do the conversion by hand is very important for understanding, there are also tools that can help you quickly find the value of degrees to radians in terms of pi. Many online calculators or software programs have a 'degrees to radians converter' feature. These tools simply apply the multiplication by π/180 for you, giving you the answer, often expressed with pi right in it. This can be quite handy for checking your work or for quick lookups, you know.

For example, if you wanted to find the value of 150 degrees in radians in terms of pi, a converter would show you that it is 5π/6 radians. If you put in 72 degrees, it would give you 2π/5 radians. These tools are pretty good for getting immediate answers, and they can handle decimal and even negative values, too. They are, in a way, a practical application of the conversion rule we have been discussing, actually.

Using such a converter can save you time, especially when you are dealing with many conversions or just need a quick check. However, it is still very beneficial to understand the underlying math – how multiplying by π/180 actually works – so you are not just relying on a black box. Knowing the process helps build a stronger grasp of how angles are measured and how radians relate to pi, which is pretty important for deeper comprehension, so.

Whether you are converting 1 degree, 75 degrees, 315 degrees, or even 330 degrees, the principle remains the same. Each degree value has a corresponding radian value that can be expressed in terms of pi, using that simple multiplication factor. This consistent relationship is what makes the system so reliable and useful for all sorts of calculations involving angles and circles.